Compact and Intuitive Data-Driven BRDF Models
(Image Comparison)

Below we compare our factored BRDF model against the reference image, Edwards et al.'s [2006] BRDF model, Lawrence et al.'s [2004] BRDF model and Bilgili et al.'s [2011] BRDF model. We also visually show the effect of adjusting the L term (i.e., the number of iterations) in our factored BRDF representation. For higher disparity, the color-coded difference images are scaled by 5. Furthermore, we show BRDF reconstruction results from the factor measurements. Finally, we show the visual comparisons of well-known BRDF parameterizations (PDV, Half-Out, Half-Diff), the factorized BRDFs by the CPD method with 1 and 10 iterative terms, the 2D BRDFs factorized by the CPD method.

◄ back to the publication web page

Jump to comparisons:

Comparison of BRDF representations

The reference image was rendered at 262144 samples / pixel:

The visual comparisons of well-known BRDF representations. The images were rendered at 262144 samples / pixel:

Comparison of difference images

The visual comparisons of the color-coded difference images of well-known BDRF representations:

Comparison of sampling efficiency

Side-by-side comparison. The images were rendered at 256 samples / pixel:

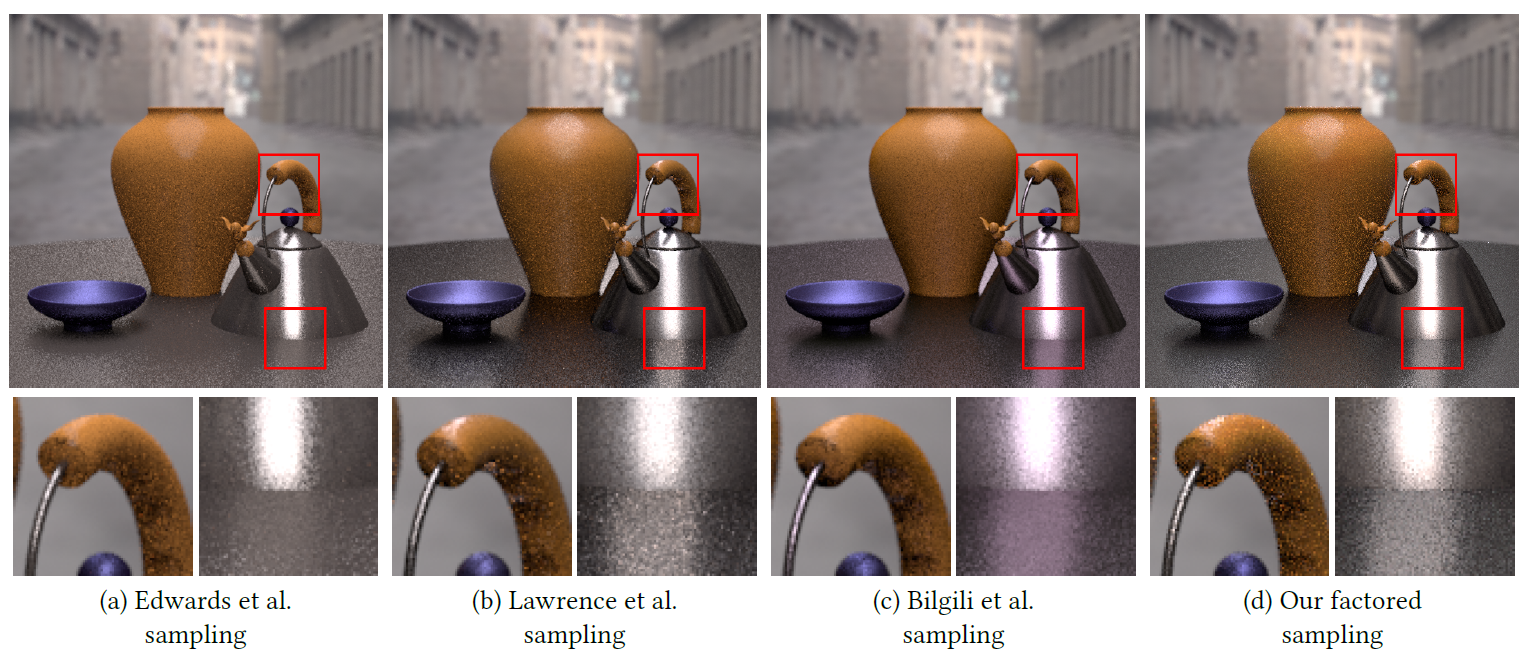
The visual comparisons of the sampling efficiency of well-known BRDF representations:

Comparison of BRDF reconstructions

The separability of the PDV parameterization is useful in BRDF measurements. We can reconstruct BRDFs by using only measurements of two parameters (θr and dp) as the Φp parameter is assumed to have little variance on isotropic BRDFs. When specular lobe measurements are captured for the function describing θr parameter, th‘e dp parameter is described by the measurements from a fixed angle of θr. The visual comparisons of BRDF reconstructions from the factor measurements can be seen in the following link:

Go to the comparison web page

Comparison of BRDF parameterizations

A general overview of well-known BRDF parameterizations:

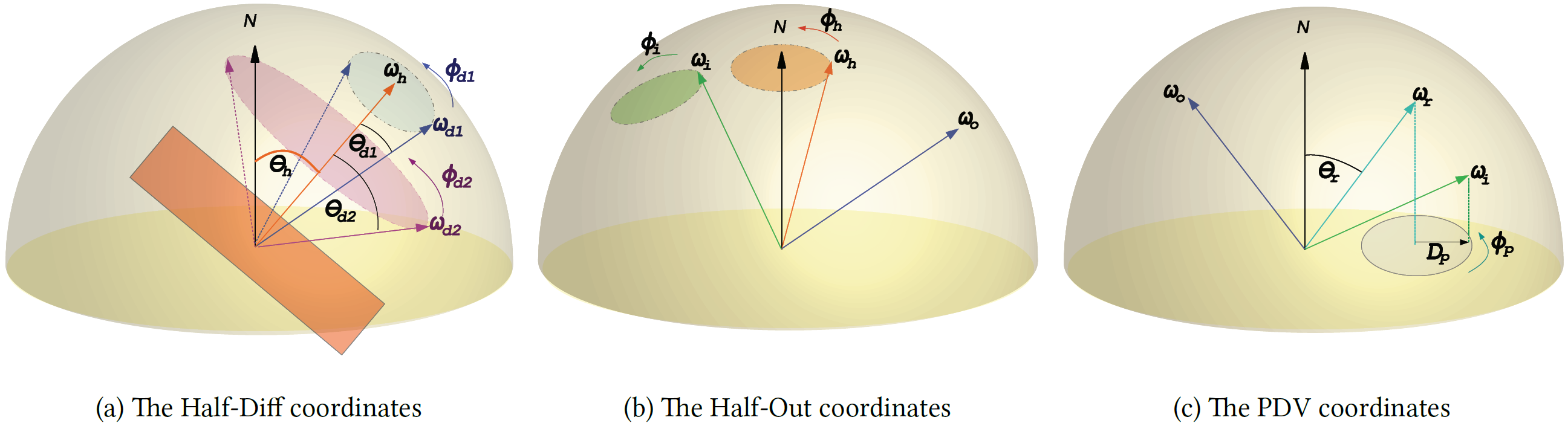
The visual comparisons of well-known BRDF parameterizations (PDV, Half-Out and Half-Diff), the factorized BRDFs by the CPD method with 1 and 10 iterative terms, the 2D BRDFs factorized by the CPD method can be seen in the following link. In the following link, each row represents rendering in each parameterization and compares against its factorized BRDF. The second and fourth columns of the rendering represent the factorized BRDFs by the CPD method with 1 and 10 iterative terms respectively. The sixth column represents the 2D BRDFs factorized by the CPD method. The third, fifth and seventh columns show the heat maps of the errors between the reference and each estimated BRDFs:

Supplemental material, PDF (48MB)